Módulo 110

TC.Fisica.Net
Módulo 110
Análise Dimensional.

Data da última atualização :

12/01/2002

1. Grandezas Físicas : (Veja página sobre grandezas físicas)

As grandezas ditas fundamentais são aquelas que podem ser medidas diretamente. Existem somente sete (7) destas grandezas : Comprimento, Massa, Tempo, Corrente elétrica, Temperatura termodinâmica, Intensidade luminosa e Quantidade de substância. Destas, interessa-nos as três primeiras, representadas da seguinte maneira : [L] = Comprimento ; [M] = Massa ; [T] = Tempo.

As grandezas derivadas são as que obtemos a partir das fundamentais, como por exemplo : Área, Densidade, Velocidade, Aceleração, Força, Impulso, Corrente elétrica, Potência, ...

2. Fórmulas Dimensionais :
Quando queremos representar a unidade de medida de uma grandeza física qualquer "G", sem especificar a que sistema de unidades ela pertence, colocamos o símbolo da grandeza entre colchetes : [G]. A partir daí, procuramos representá-la através de suas grandezas fundamentais : [L], [M], [T]. Estas representações são denominadas fórmulas dimensionais e os expoentes das unidades fundamentais, dimensões.
Exemplos :

3. Equações homogêneas :
Somente podemos comparar grandezas de mesma espécie, ou seja, em uma equação física qualquer, os dois membros da igualdade precisam ter as mesmas dimensões. Quando isto acontecer dizemos que a equação é homogênea. A homogeneidade de uma equação é, portanto, um critério de verificação de sua validade. Porém devemos lembrar que a análise dimensional não permite verificar se eventuais constantes adimensionais (números puros) são corretos. Então a homogeneidade de uma equação é uma condição necessária mas não suficiente para que a equação seja correta.
Exemplo : Verificar a homogeneidade da equação de energia potencial elástica :

1° termo : Energia	2° termo : Equação

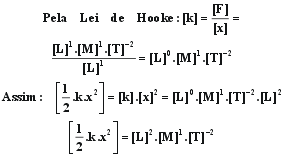Observe que os dois termos chegam ao mesmo resultado, portanto a equação é homogênea, mas, nada podemos garantir quanto ao fator "1/2" da equação de Energia Potencial Elástica.