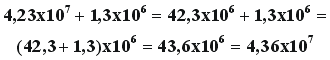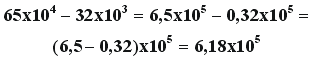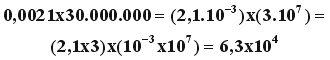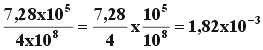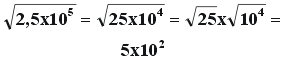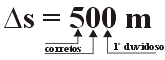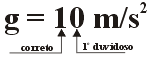Módulo 109

TC.Fisica.Net
Módulo 109
Algarismos Significativos : Notação científica, Algarismos significativos e Ordem de grandeza.

Data da última atualização :

10/01/2002

1. Potências de Dez (Notação científica) :

"Um número qualquer pode sempre ser expresso como o produto de um número compreendido entre "1" e "10", por uma potência de 10 adequada."

Transformando um número em potência ou uma potência em número :
	Movendo a vírgula para a esquerda o expoente da potência é somado :
	Exemplos :	357.400 = 3,574 x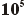
	1.254 x 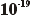= 1,254 x	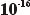107 x 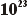= 1,07 x
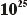	Movendo a vírgula para a direita o expoente da potência é subtraído :
	Exemplos :	0,005 = 5,0 x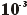
	0,00016 x 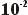= 1,6 x	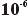0,08 x 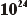= 8,0 x

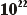Operações com potência de dez :
	Soma e Subtração : Os número devem apresentar potências de mesmo expoente, que serão colocadas em evidência :
	Exemplo de soma :

	Exemplo de subtração :

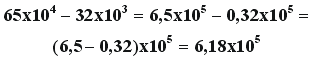	Multiplicação, Divisão e Radiciação : Efetuar as operações de números e potências separadas, juntando-os apenas no final :
	Exemplo de multiplicação :

	Exemplo de divisão :

	Exemplo de radiciação :

2. Algarismos Significativos :

"São todos os algarismos corretos de um número mais o primeiro duvidoso."

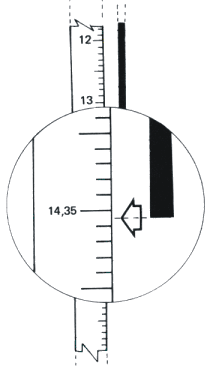
Para entender o que é um algarismo duvidoso, observe a medida feita com uma régua milimetrada (figura à es-querda) . Podemos observar que a lei-tura corresponde a um valor entre 14,3 e 14,4 cm. Assim, um provável valor seria : 14,35 cm. Os algarismos "1" , "4" e "3" foram lidos direta-mente na régua, por isto são conside-rados corretos. O algarismo "5" foi "chutado", portanto é considerado du-vidoso. Neste caso, temos 4 algarismos significativos.

Na figura à direita realizamos a mes-ma medida anterior, mas a régua uti-lizada possui escala de décimos de milímetros. Observamos que a leitura agora é um valor entre 14,35 e 14,36 mm. Uma possibili- dade é 14,356. Os algarismos "1" , "4", "3" e "5" foram lidos diretamente na régua, por isto são considerados corretos. O algarismo "6" foi "chutado, portanto é duvidoso. Nesta outra régua, temos 5 algarismos significativos.


Regras para a determinação do número de algarismos significativos :
	1) Número fornecido : Quando um número é fonecido em um texto teórico ou de exercícios, o algarismo duvidoso é o que se encontra mais à direita. Todos os demais são corretos.
	Exemplos :


	2) Zeros à esquerda : Não são contados como significativos.
	Exemplos :


	3) Zeros à direita ou intermediários : São considerados significativos.
	Exemplos :


	4) Potências de dez : Não são consideradas significativas.
	Exemplos :



	5) Valores com desvio absoluto médio expresso : Deve-se contar todos os algarismos até o primeiro duvidoso apresentado no desvio.
	Exemplos :

Operações com algarismos significativos :
	1) Soma e subtração : Todos os números devem possuir o mesmo número de casas decimais (o menor). Para aproximação, comparar com "5".
	2.807,5	não se altera .........................	2.807,5
	+ 0,0648	transforma-se em .................	+ 0,1
	+ 83,645	transforma-se em .................	+ 83,6
	+ 525,35	transforma-se em .................	+ 525,3

	Resultado final ..........................................................		3.416,5

	2) Multiplicação e Divisão : A operação deve ser efetuada normalmente e o resultado final deve possuir o mesmo número de algarismos significativos do menor. Para aproximação, comparar com "5".
	3,67 x 2,3 = 8,441 = 8,4 = 2 a.s. (número de algarismos de "2,3")
	123 x 0,5 = 61,5 = 6 . 10² = 1 a.s. (número de algarismos de "0,5")
	123,7 x 2,99 = 369,863 = 370 = 3 a.s. (número de algarismos de "2,99")

3. Ordem de Grandeza :
"É a potência de dez mais próxima do número apresentado. Deve-se proceder uma aproximação, comparando com ."
	Exemplos :