TC.Fisica.Net
Módulo
062
Ondas
: Conceitos básicos de onda senoidal.
Data da última atualização : 04/01/2002
|
Onda
(Definição) : Qualquer
perturbação de uma grandeza física associada
a um meio material e que se propaga através dele.
|
|
|
|
 As ondas produzidas pela queda da esfera são perturbações de pressão da água que propagam em sua superfície. |
|
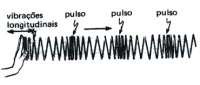
Propriedade fundamental : Uma onda nunca arrasta o meio material em que se propaga. Apenas o faz vibrar. Exemplos : Um surfista não é levado pela onda do mar e sim pelo excesso de água vibrada por ela em pequenas profundidades; O som não movimenta o ar atmosférico em que se propaga, apenas o vibra. Na figura seguinte, observe que o ponto "P" não muda sua posição horizontal a medida que a onda passa por ele e sim vibra verticalmente. |
|
 |
|
|
Lei
da Velocidade : Uma
onda sempre se move em Movimento Retilíneo
e Uniforme (MRU) dentro de um único meio. Sua velocidade
somente se altera se ela mudar de meio material onde se propaga.
|
||||
|
Classificação das ondas : |
||||
| 1* Quanto à Natureza : | ||||
| * Mecânica : Necessita obrigatoriamente de meio material para se propagar. Ex.: Onda na água, Onda na corda, Som... | ||||
| * Eletromagnética : Pode se propagar nos meio material e no vácuo. Ex.: Ondas de rádio, Microondas, Luz... | ||||
| 2* Quanto à Forma : | ||||
| * Longitudinal : Onda que vibra na mesma direção em que se propaga. Ex.: Som no ar, Onda em mola,... |
 |
 |
||
| * Transversal : Onda que vibra perpendicularmente à direção de propagação. Ex.: Luz, Onda na corda,... |
|
 |
||
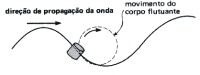
| * Mista : Onda que vibra na mesma direção e perpendicularmente à direção de propagação, simultaneamente. Ex.: Onda na água, Som nos sólidos,... |
 |
 |
||
| 3* Quanto à Frente de onda : | ||||
| * Puntiforme : Onda produzida na corda. |
|
|||
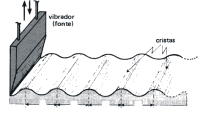
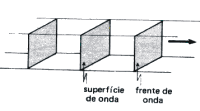
| * Reta : Onda criada na água pelo movimento ascendente e descendente de um vibrador reto, perpendicular à superfície da água. |
 |
|||
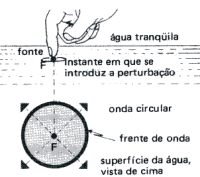
| * Circular : Onda criada na água quando tocamos a ponta do dedo em sua superfície. |
 |
|||
| * Plana : Onda luminosa solar vista da Terra. |
 |
|||
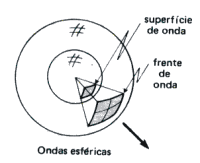
| * Esférica : Onda sonora provocada pelo estouro de uma bombinha no ar. |
 |
|||
| 4* Quanto ao número de dimensões : | ||||
| * Unidimensional : São as puntiformes. | ||||
| * Bidimensional : São as retas e circulares. | ||||
| * Tridimensional : São as planas e esféricas. | ||||
|
Estudo
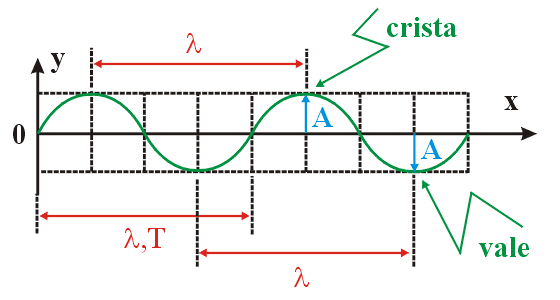
matemático de uma onda Senoidal : Uma
onda senoidal é assim denominada porque seu aspecto se assemelha
ao gráfico da função seno. Podemos obtê-la
facilmente executando um movimento de sobe-e-desce na extremidade
de uma corda.
|
||
 |
||
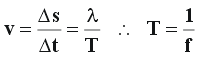 |
 |
|
|
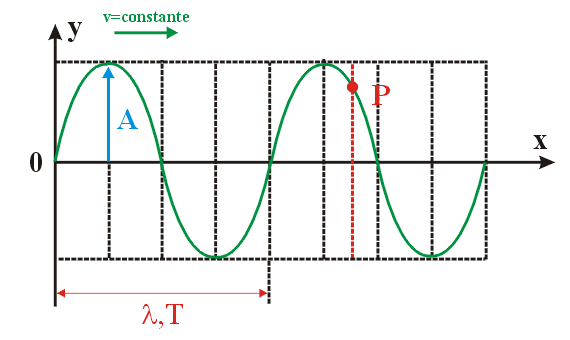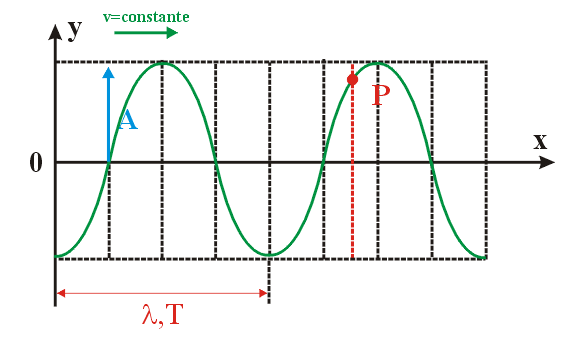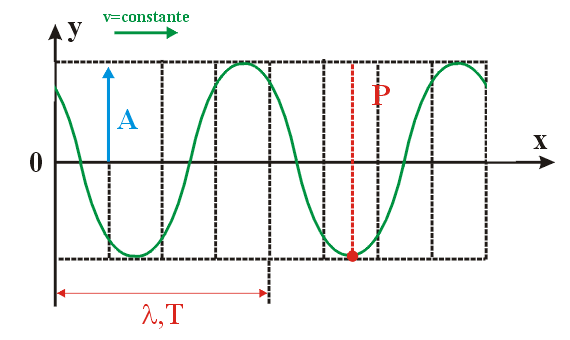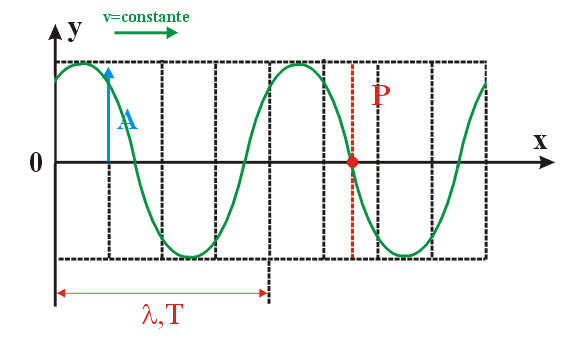
Onda
Harmônica : Uma
onda senoidal regular, ao se propagar dentro de um meio material,
faz vibrar os pontos deste meio. Na figura seguinte, enquanto a
onda se desloca com velocidade constante, o ponto "P"
executa MHS de amplitude igual à amplitude da onda. Podemos,
então, medir sua posição "y", vertical,
em cada instante através da equação de onda
harmônica (Regular).
|
|
 |
|
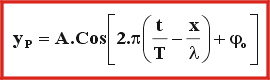 |
|
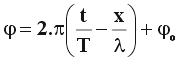 |
Fase
dos pontos de uma onda : A
fase corresponde a todo
o trecho da equação de onda harmônica dentro
dos colchetes, ou seja, é um ângulo associado à
onda indicando sua posição num determinado instante.
|
 |
|
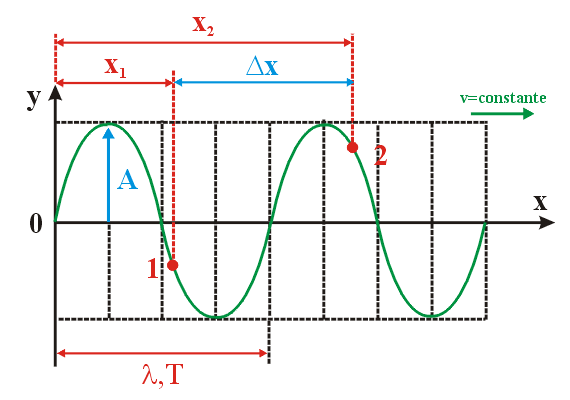
| A fase de cada ponto (1) e (2) na figura anterior podem ser calculadas da seguinte maneira : |
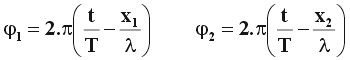 |
| Diferença de fase entre dois pontos de uma onda : A diferença entre as fases dos pontos (1) e (2) será : |
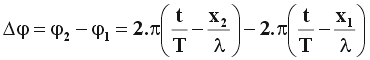 |
| Desenvolvendo a equação de cálculo de defasagem ou diferença de fase teremos : |
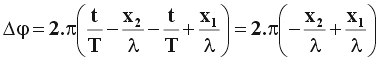 |
| O resultado final deste cálculo nos levará à seguinte expressão : |
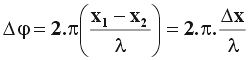 |
| Observe na figura anterior que Dx é a distância horizontal entre os pontos (1) e (2) enquanto que l é o comprimento de onda da onda. Chegaremos à seguinte conclusão : | |
|
|
Se a defasagem entre dois pontos for múltiplo par de "p", então, estarão em concordância de fase. Exemplos: Dj = 0, 2p, 4p, 6p... |
|
|
Se a defasagem entre dois pontos for múltiplo ímpar de "p/2", então, estarão em oposição de fase. Exemplos: Dj = p, 3p, 5p, 7p... |







