TC.Fisica.Net
Módulo
060
Movimento Harmônico
Simples : Energias no MHS.
Data da última atualização : 02/01/2002
|
Para
qualquer sistema mecânico podemos associar energias em seus
movimentos. No MHS não é diferente. Vamos analisar
três tipos de energia que podemos associar a este movimento
: Energia Cinética, Energia Potencial e Energia Mecânica.
|
|
|
|
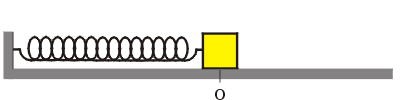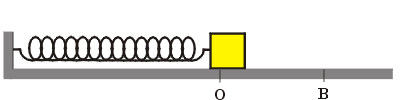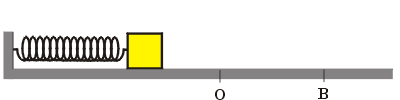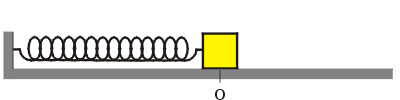
Para mostrar estas energias, imaginemos um arranjo experimental onde uma mola tem uma extremidade presa a uma parede vertical e a outra presa a um bloco de massa "m" que repousa sobre um plano horizontal perfeitamente liso (Figura animada acima). Quando retiramos o bloco de sua posição de equilíbrio (O), levamos até um ponto mais à direita "B" e o soltamos, devido à força exercida pela mola, ele executará MHS entre os extremos "C" e "B", tendo o ponto "O" como origem (zero) e referência. Neste experimento, quando o bloco tiver velocidade, acumulará Energia Cinética. Quando a mola tiver deformação, acumulará Energia Potencial Elástica e somando as duas energias obteremos a Energia Total ou Energia Mecânica. |
|
Distribuição de Energia em função da elongação do MHS : Na figura abaixo, mostramos o comportamento das energia acumuladas durante uma oscilação do sistema massa-mola. Observe que nas extremidades "C" e "B" a velocidade do bloco é nula implicando em Energia cinética também nula. Por outro lado, nestes mesmos pontos, a deformação da mola é máxima implicando que a Energia Potencial Elástica é máxima. Por fim, nos extremos a Energia Mecânica é totalmente potencial, pois não existe a Cinética. Utilizando o mesmo raciocínio anterior, no ponto central "O" a deformação da mola é nula e sua Energia Potencial Elástica é nula. Sua Energia Cinética é máxima pois o bloco passa por "O" com a maior velocidade da trajetória e a Energia Mecânica é exclusivamente Cinética pois a Potencial é nula. |
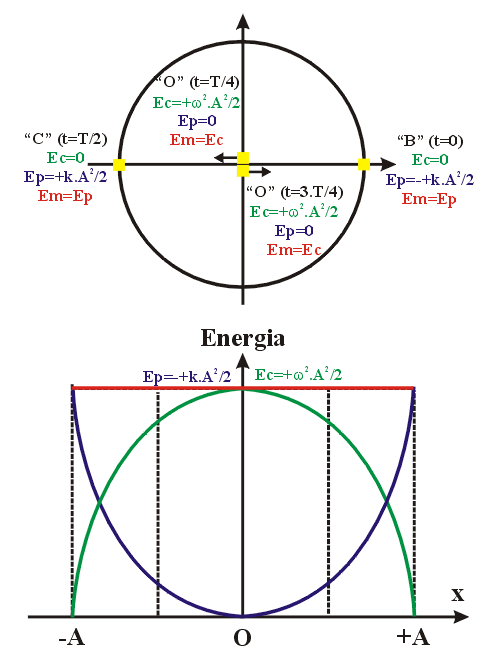 |
| Finalizando a análise energética do MHS, lembramos que o exemplo mostrado é do tipo conservativo, ou seja, não apresenta forças dissipativas, mantendo constante sua Energia Mecânica durante todo o movimento. Esta constância está mostrada no gráfico anterior através da reta vermelha horizontal. Para qualquer ponto do gráfico (x) a soma da Energia Cinética com a respectiva Energia Potencial, no mesmo ponto, resultará no mesmo valor, a Energia Mecânica, neste caso, constante. |