TC.Fisica.Net
Módulo 006
Movimento Retilíneo Uniformemente Variado (MRUV) : Análise Gráfica.

Data da última atualização : 05/04/2002

Gráficos : É possível estabelecer a relação gráfica das grandezas envolvidas no estudo do MRUV, a saber : "s x t" , "v x t" e "a x t", apresentados a seguir :

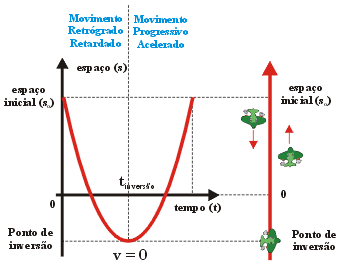
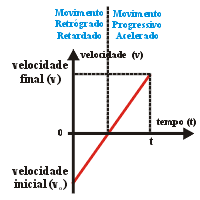
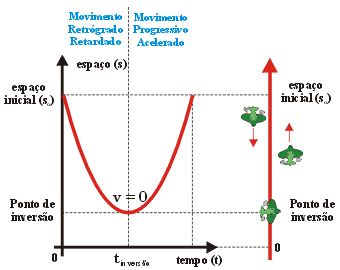
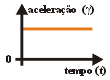
Movimento retilíneo iniciado em espaço escalar positivo, contra a orientação da trajetória, indicando velocidade escalar negativa decrescente até o ponto de inversão. A partir dele, o espaço escalar e a velocidade voltam a crescer. Durante todo o movimento a aceleração escalar é positiva.
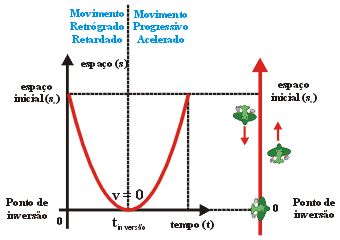
Movimento retilíneo iniciado em espaço escalar positivo, contra a orientação da trajetória, indicando velocidade escalar negativa decrescente até o ponto de inversão, que coincide com a origem da trajetória. A partir dele, o espaço escalar e a velocidade voltam a crescer. Durante todo o movimento a aceleração escalar é positiva.
Movimento retilíneo iniciado em espaço escalar positivo, contra a orientação da trajetória, indicando velocidade escalar negativa decrescente até o ponto de inversão. A partir dele, o espaço escalar e a velocidade voltam a crescer. Durante todo o movimento a aceleração escalar é positiva.
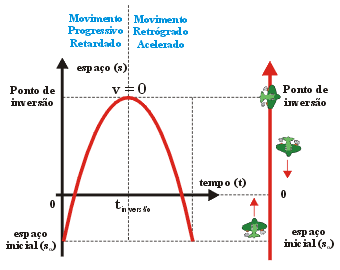
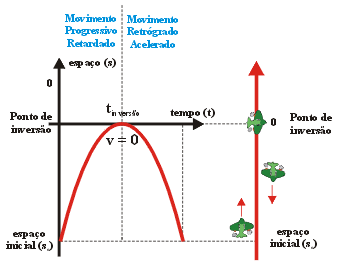
Movimento retilíneo iniciado em espaço escalar negativo, a favor da orientação da trajetória, indicando velocidade escalar positiva decrescente até o ponto de inversão. A partir dele, o espaço escalar decresce e a velocidade volta a crescer. Durante todo o movimento a aceleração escalar é negativa.
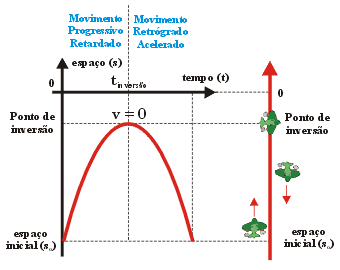
Movimento retilíneo iniciado em espaço escalar negativo, a favor da orientação da trajetória, indicando velocidade escalar positiva decrescente até o ponto de inversão, que coincide com a origem da trajetória. A partir dele, o espaço escalar decresce e a velocidade volta a crescer. Durante todo o movimento a aceleração escalar é negativa.
Movimento retilíneo iniciado em espaço escalar negativo, a favor da orientação da trajetória, indicando velocidade escalar positiva decrescente até o ponto de inversão. A partir dele, o espaço escalar decresce e a velocidade volta a crescer. Durante todo o movimento a aceleração escalar é negativa.

Outros casos gráficos : É possível encontrarmos outros movimentos diferentes dos apresentados anteriormente. Nos gráficos seguintes procuramos enumerar estes casos.

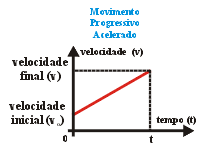
		Movimento retilíneo sempre a favor da orientação da trajetória, iniciando com velocidade escalar positiva, crescente, indicando que não haverá ponto de inversão. Durante todo o movimento a aceleração escalar é positiva.
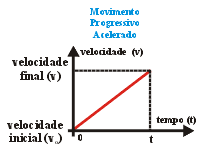
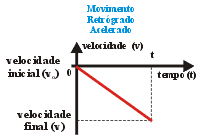
		Movimento retilíneo sempre a favor da orientação da trajetória, iniciando com velocidade escalar nula, crescente, indicando que não haverá ponto de inversão. Durante todo o movimento a aceleração escalar é positiva.
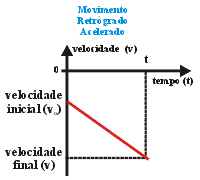
		Movimento retilíneo sempre contra a orientação da trajetória, iniciando com velocidade escalar nula, crescente, indicando que não haverá ponto de inversão. Durante todo o movimento a aceleração escalar é negativa.
		Movimento retilíneo sempre contra a orientação da trajetória, iniciando com velocidade escalar negativa, crescente, indicando que não haverá ponto de inversão. Durante todo o movimento a aceleração escalar é negativa.

Propriedades Gráficas : Para os gráficos mostrados anteriormente, encontramos duas propriedades :

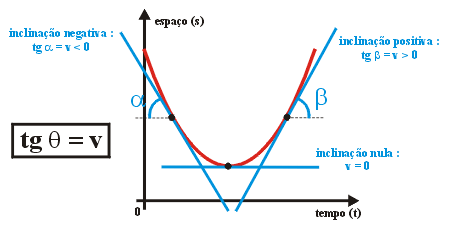
1° : Gráfico de espaço em função do tempo ("s x t") :
Para um movimeto uniformemente variado, a tangente de inclinação da reta que corta a parábola no gráfico de espaço por tempo ("s x t") indica o valor da velocidade naquele instante. No gráfico ao lado a inclinação crescente indica velocidade positiva, inclinação decrescente indica velocidade negativa e no ponto de inversão, como a inclinação é nula, a velocidade também será.
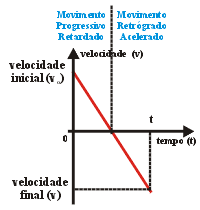
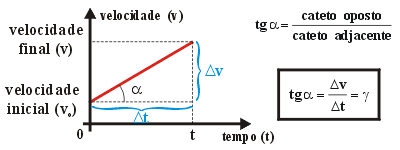
2° : Gráfico de velocidade em função do tempo ("v x t") :
Para um movimento representado, a tangente da inclinação do gráfico fornece o valor da aceleração (constante). Neste caso a inclinação é positiva (crescente) indicando aceleração positiva. Outra possibilidade seria a inclinação decrescente, indicando aceleração negativa.
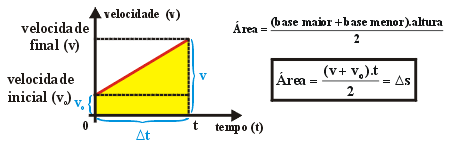
No mesmo gráfico de velocidade mostrado anteriormente, poderíamos calcular a área abaixo dele até o eixo dos tempos, correspondente a um trapézio. Este valor corresponde à variação de espaço do móvel durante o movimento.
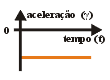
3° : Gráfico de aceleração em função do tempo ("g x t") :
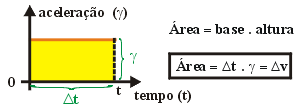	No gráfico de aceleração, podemos calcular a área abaixo dele até o eixo dos tempos, correspondente a um retângulo. Este valor corresponde à variação de velocidade do móvel durante o movimento.
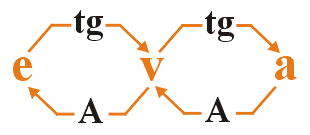Resumindo : No gráfico de espaço, a tangente da inclinação fornece a velocidade, no gráfico de velocidade a tangente da inclinação fornece a aceleração, no gráfico de aceleração, a área até o eixo dos tempos fornece a variação de velocidade e no gráfico de velocidade, novamente, a área até o eixo dos tempos fornece a variação de espaço do movimento. Veja esquema ao lado.