TCFisicaNet
Regras de Derivação

A derivação é uma operação matemática que possui centenas de regras, dependendo da função matemática utilizada. Desejamos apresentar neste tópico apenas as regras de derivação para funções lineares.

1ª Regra : A derivada de constante (número) é zero : Ex.: s = 2 ; ds/dt = 0;

2ª Regra : A derivada de função com expoente é : Ex.: s = k.tⁿ ; ds/dt = n.k.t^n-1;

A segunda regra pode parecer complicada, mas vamos tentar facilitar. A figura mostra os passos para aplicar esta regra. 

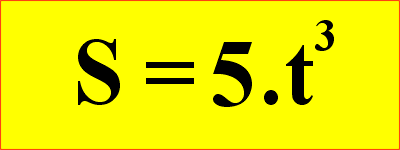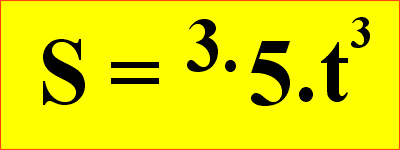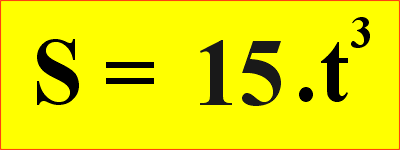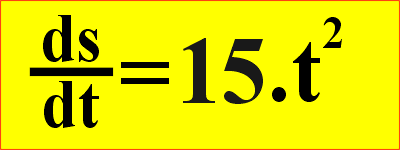
Primeiro baixamos o expoente (n), que vale "3" e multiplicamos por "k" que vale "5". Em seguida diminuímos uma unidade no expoente (n) que passa a valer "2".

Pronto. A derivação da equação de espaço (s) foi completada. Experimente fazer com a equação seguinte que apresenta vários termos. 

Acompanhe como baixamos o expoente e o reduzimos em uma unidade. A derivada de "7" é zero, portanto é excluído da equação. "t" tem expoente "1" e quando subtraído de uma unidade fica elevado a zero, cujo resultado é "1" e portanto também "some" da equação.

A derivada da função de espaço é a velocidade, da função de velocidade é a aceleração e a derivada de aceleração é chamado de "tranco" ou "sacudida" e indica o quanto varia a aceleração em função do tempo. Acompanhe o esquema gráfico mostrando a sequência de derivação.